傳統(tǒng)的試驗(yàn)方法研究材料的宏觀形變行為已非常成熟,但采用該方法存在試驗(yàn)周期長(zhǎng)、成本高等不足,并且無(wú)法直接觀測(cè)材料內(nèi)部的微觀形變及力學(xué)行為。因此,為了降低材料特性研究時(shí)對(duì)試驗(yàn)的過(guò)分依賴,可描述多晶相互作用的晶體塑性理論及分子動(dòng)力學(xué)理論得以發(fā)展。并且,近年來(lái)計(jì)算機(jī)性能的提升也加速了基于晶體塑性理論或分子動(dòng)力學(xué)理論的金屬材料形變特性的研究進(jìn)程。但是,晶體塑性有限元理論多用于模擬晶粒級(jí)細(xì)觀尺度下的形變行為,無(wú)法體現(xiàn)材料在形變過(guò)程中的原子構(gòu)型及位錯(cuò)的演化,而用于描述原子在外力作用下最基本運(yùn)動(dòng)細(xì)節(jié)的分子動(dòng)力學(xué)模擬則可以彌補(bǔ)這一短板。分子動(dòng)力學(xué)模擬需依據(jù)材料經(jīng)驗(yàn)力場(chǎng)及原子初始位置計(jì)算其勢(shì)能,通過(guò)求導(dǎo)的方法分析體系內(nèi)各個(gè)原子的受力情況,進(jìn)而基于牛頓運(yùn)動(dòng)方程,在極短的時(shí)間間隔(1×10-15s)內(nèi)計(jì)算原子新的位置及受力,如此反復(fù)直至計(jì)算收斂[1-2]。因此,分子動(dòng)力學(xué)模擬可以實(shí)時(shí)捕捉體系的動(dòng)態(tài)形變,為在原子尺度上研究微觀形變機(jī)制奠定了基礎(chǔ)。ChenB等[3]建立了具有多種取向位錯(cuò)網(wǎng)的單晶鎳基高溫合金的分子動(dòng)力學(xué)模型,通過(guò)對(duì)比體系能量及位錯(cuò)網(wǎng)演化過(guò)程,為建立更加精確的界面位錯(cuò)網(wǎng)模型提供依據(jù)。之后,LiNL和WuWP等[4]對(duì)引入界面位錯(cuò)網(wǎng)的分子動(dòng)力學(xué)模型施加單軸拉伸載荷及循環(huán)載荷,通過(guò)分析材料形變過(guò)程中的位錯(cuò)演化、層錯(cuò)/滑移運(yùn)動(dòng)及應(yīng)力-應(yīng)變行為,評(píng)估應(yīng)變率、溫度對(duì)材料力學(xué)行為及循環(huán)形變機(jī)制的影響。LiXT等[5]揭示了位錯(cuò)發(fā)射與孔洞和缺陷的相互作用機(jī)理,認(rèn)為位錯(cuò)發(fā)射會(huì)導(dǎo)致裂紋尖端鈍化,是裂紋尖端脆性擴(kuò)展演化為韌性擴(kuò)展的主要因素。祝占偉[6]采用分子動(dòng)力學(xué)模擬分析了鎳基合金中五重孿晶的形成機(jī)制及形變機(jī)理。本文建立了LAMMPS分子動(dòng)力學(xué)仿真原子結(jié)構(gòu)模型,進(jìn)行了室溫(300K)與高溫(600和920K)條件下的單軸拉伸仿真,討論了溫度對(duì)模型內(nèi)部位錯(cuò)演化及力學(xué)行為的影響。

1、分子動(dòng)力學(xué)模型

1.1　相互作用勢(shì)函數(shù)

本文采用嵌入原子法(Embedded-AtomMethod,EAM)勢(shì)函數(shù)[7]來(lái)描述原子間作用力的相互作用,EAM勢(shì)是一種描述金屬鍵最常用、最精確的相互作用模型,并且常用于描述原子尺度下的擴(kuò)散、變形、熔化和燒結(jié)等過(guò)程[8-10]。EAM勢(shì)中總能量Etot的計(jì)算公式如下,其中,系數(shù)1/2是為了避免一對(duì)相互作用的重復(fù)計(jì)算。

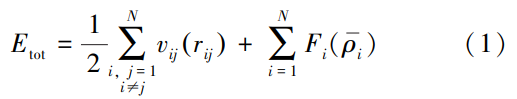
式中:vij(rij)為分離距離為rij的原子i與原子j之間的一對(duì)相互作用能;Fi為原子i的嵌入能,可以描述為局部電子密度ρi的函數(shù);N為體系內(nèi)共參與計(jì)算的原子對(duì)的數(shù)量。ρi的表達(dá)式為:

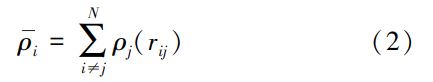
式中:ρj(rij)為將原子i賦值到分離距離為rij的原子j的電子密度函數(shù)。采用用于表示接近等原子成分組成下的Fe-NiCr-Co-Al的高度理想化面心立方FCC混合物的EAM勢(shì)函數(shù)[7],該EAM勢(shì)旨在模擬復(fù)雜系統(tǒng)的性質(zhì),可以較為精確地模擬系統(tǒng)中各類原子之間的相互作用。

1.2　原子結(jié)構(gòu)模型

GH4169鎳基高溫合金粉末中存在超過(guò)10種元素,而Ni、Cr、Al與Fe元素的占比超過(guò)了元素總體含量的90%(質(zhì)量百分?jǐn)?shù))。因此,為了在簡(jiǎn)化原子結(jié)構(gòu)模型建模的同時(shí),盡可能地保證多體相互作用的準(zhǔn)確性,建立GH4169鎳基高溫合金原子結(jié)構(gòu)模型時(shí)僅考慮Ni、Cr、Al與Fe共4種主要元素[9],4種元素的含量分別為52%、10%、1%與37%,即Ni52Fe37Cr10Al1。由于GH4169鎳基高溫合金中Ni元素含量最多,因此,在后續(xù)建模過(guò)程中,首先,依據(jù)鎳基合金晶體類型建立適當(dāng)尺寸的面心立方結(jié)構(gòu)Ni單晶晶格模型。然后,依據(jù)Cr、Al與Fe這3種元素占比,分別在Ni單晶晶格模型中的FCC格位上隨機(jī)替換Ni原子,形成一種高度類似于GH4169鎳基高溫合金元素組成的Ni52Fe37Cr10Al1原子結(jié)構(gòu),用于后續(xù)分子動(dòng)力學(xué)計(jì)算。需要說(shuō)明的是,Ni元素的點(diǎn)陣常數(shù)aNi=3.52?作為常數(shù)用于后續(xù)建模。計(jì)算原子尺度下的GH4169鎳基高溫合金單軸拉伸應(yīng)力-應(yīng)變關(guān)系時(shí),首先,建立尺寸(無(wú)量綱)為40×40×40的面心立方結(jié)構(gòu)Ni單晶晶格模型,結(jié)合Ni元素的點(diǎn)陣常數(shù)可知,該晶格模型在x、y與z方向上的實(shí)際尺寸分別為40aNi、40aNi與40aNi。最終模型包含的原子總數(shù)為256000個(gè),其中Ni原子有133120個(gè)、Fe原子有94720個(gè)、Cr原子有25600個(gè)、Al原子有2560個(gè),最終模型如圖1所示。

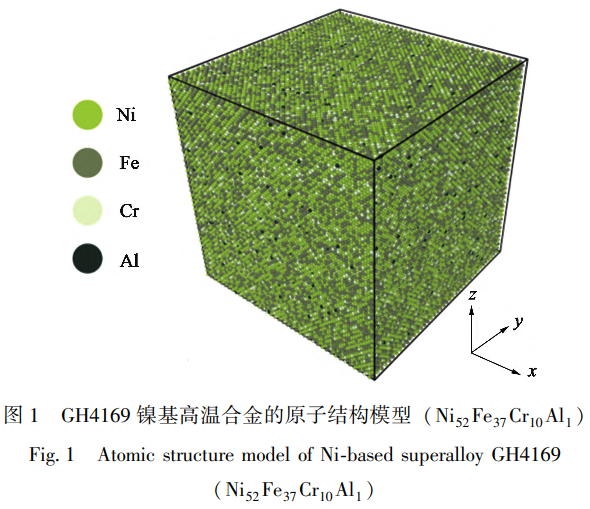
施加單軸拉伸載荷之前,首先在NVE(原子數(shù)-體積能量,Number-Volume-Energy)系綜(恒定原子序數(shù),恒溫,不恒壓)下對(duì)模型弛豫50ps,保證系統(tǒng)處于平衡狀態(tài)。然后,利用Nose-Hoover熱浴法設(shè)置環(huán)境溫度,并且通過(guò)NVT(原子數(shù)-體積-溫度,Number-Volume-Temperature)系綜用應(yīng)變控制對(duì)原子結(jié)構(gòu)模型施加單軸拉伸載荷,應(yīng)變率為1×109s^-1。計(jì)算過(guò)程中每間隔5ps輸出環(huán)境熱力學(xué)信息,以監(jiān)控仿真是否平穩(wěn)運(yùn)行。通過(guò)設(shè)置變量的方法計(jì)算不同時(shí)刻體系的應(yīng)力與應(yīng)變數(shù)值,以繪制應(yīng)力-應(yīng)變曲線。仿真過(guò)程時(shí)間步長(zhǎng)為0.001ps,每隔5ps輸出體系形變結(jié)果。此外,通過(guò)改變環(huán)境溫度(300、600和920K),以探究溫度對(duì)GH4169鎳基高溫合金應(yīng)力應(yīng)變關(guān)系的影響。需要說(shuō)明的是,整體計(jì)算過(guò)程包含minimize過(guò)程、弛豫過(guò)程、fix-deform過(guò)程,拉伸載荷加載過(guò)程中以載荷施加完畢為形變過(guò)程結(jié)束時(shí)刻,因此,并未關(guān)注整體計(jì)算時(shí)間。5000個(gè)時(shí)間步長(zhǎng)是為了降低計(jì)算結(jié)果文件體積的同時(shí)保證輸出計(jì)算結(jié)果可以精確反應(yīng)整體形變過(guò)程。

2、結(jié)果與討論

2.1　不同溫度下的微觀應(yīng)力-應(yīng)變關(guān)系

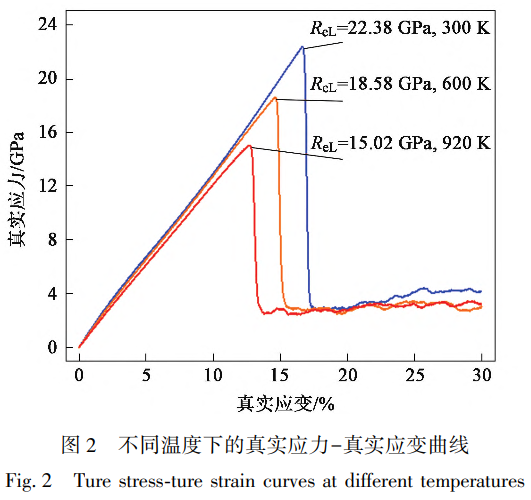
為了探究原子級(jí)納米尺度下溫度對(duì)GH4169鎳基高溫合金單軸拉伸力學(xué)性能及形變機(jī)制的影響,在300、600和920K條件下對(duì)原子結(jié)構(gòu)施加單軸拉伸載荷,計(jì)算得到的真實(shí)應(yīng)力-真實(shí)應(yīng)變曲線,如圖2所示。研究表明,分子動(dòng)力學(xué)模擬過(guò)程中應(yīng)變率的大小對(duì)材料彈性行為的影響可以忽略,更高的應(yīng)變率僅表現(xiàn)出更高的屈服強(qiáng)度與更差的塑性[4]。從圖2中可以看,不同溫度下的真實(shí)應(yīng)力-真實(shí)應(yīng)變曲線均可劃分為3個(gè)區(qū)域,即隨著應(yīng)變的增加,依次為應(yīng)力線性增加的彈性區(qū)、應(yīng)力驟降的塑性激活區(qū)與應(yīng)力穩(wěn)定的應(yīng)力釋放區(qū)[11]。與宏觀應(yīng)力-應(yīng)變曲線不同的是,微觀尺度下的應(yīng)力-應(yīng)變曲線在進(jìn)入塑性激活區(qū)后應(yīng)力變化呈現(xiàn)先驟降后波動(dòng)的特征,這是因?yàn)樵谶M(jìn)入屈服階段后原子結(jié)構(gòu)內(nèi)部會(huì)形成大量位錯(cuò),隨著應(yīng)變的增加,位錯(cuò)會(huì)增殖與運(yùn)動(dòng),因此,位錯(cuò)與位錯(cuò)之間、位錯(cuò)與其他晶體學(xué)結(jié)構(gòu)之間會(huì)出現(xiàn)相互作用,這些相互作用一定程度上會(huì)使位錯(cuò)塞積,甚至消失,最終導(dǎo)致應(yīng)力波動(dòng)。應(yīng)力驟降是由于Shockley位錯(cuò)發(fā)生反應(yīng),演化為其他類型位錯(cuò)或泯滅,此時(shí)體系內(nèi)應(yīng)力釋放,導(dǎo)致應(yīng)力下降。此外,隨著溫度的升高,GH4169鎳基高溫合金的屈服強(qiáng)度ReL逐漸下降,分別為22.38、18.58和15.02GPa。同樣地,屈服應(yīng)變也隨溫度的升高而降低,分別為16.65%、14.63%和12.67%,這表明溫度越高,納米原子GH4169鎳基高溫合金結(jié)構(gòu)越容易形成位錯(cuò),導(dǎo)致塑性形變。利用不同溫度下彈性區(qū)的真實(shí)應(yīng)力-真實(shí)應(yīng)變曲線擬合得到的彈性模量分別為125.9、125.3和119.1GPa,可以看出,當(dāng)溫度低于920K時(shí),材料的彈性模量十分接近,而當(dāng)溫度達(dá)到920K時(shí),彈性模量下降了6.8GPa,這從納米尺度上證明了GH4169鎳基高溫合金具有良好的920K高溫抗性。

2.2　形變過(guò)程中原子構(gòu)型演化

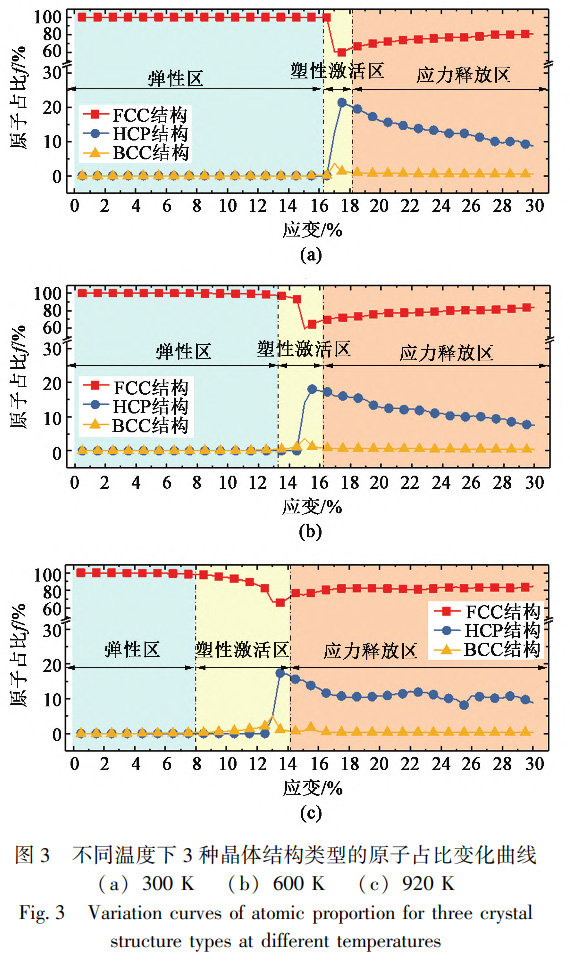
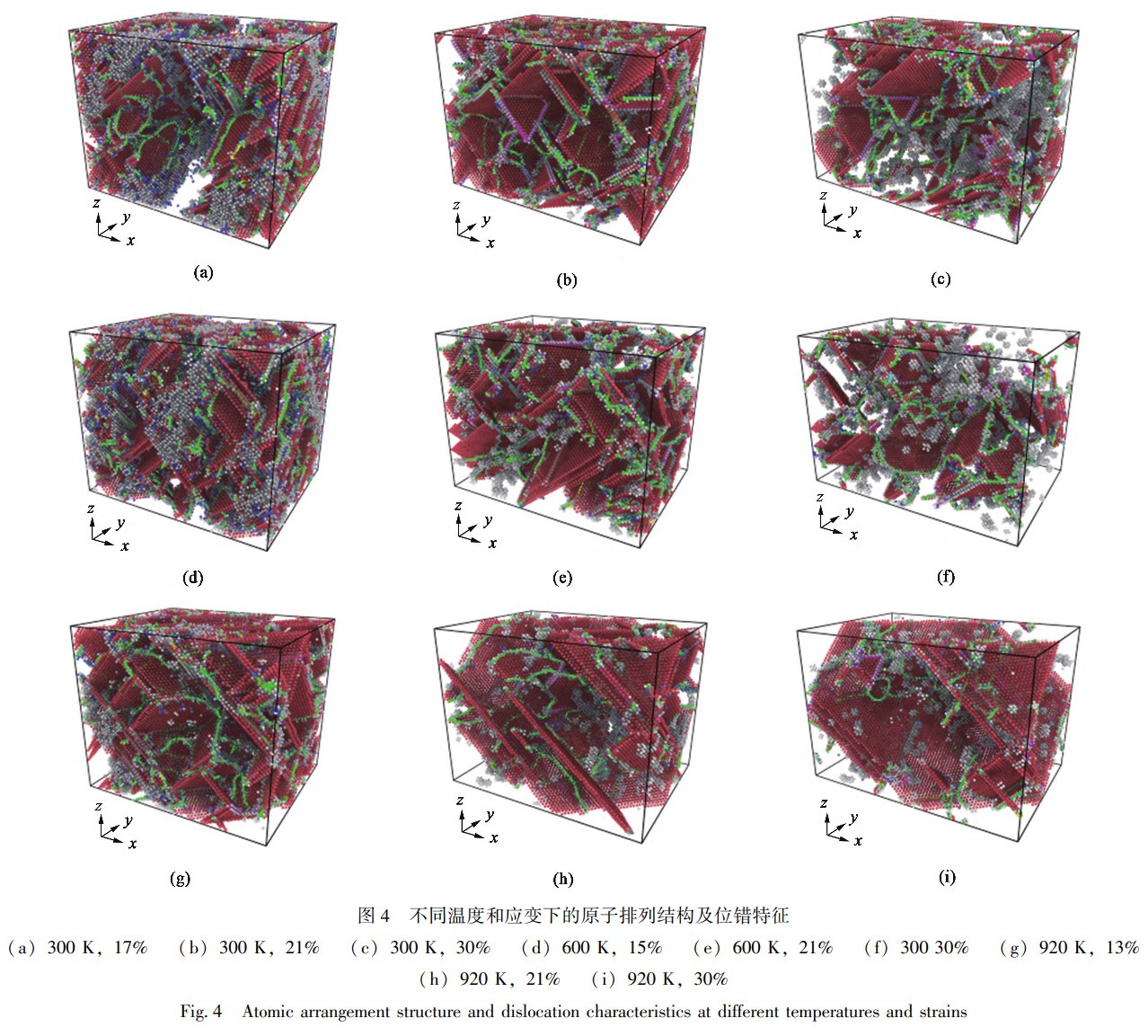
圖3為不同溫度下隨應(yīng)變?cè)黾釉咏Y(jié)構(gòu)模型中3種不同晶體結(jié)構(gòu)類型的原子占比變化情況。從圖3中可以看出,形變初期3種晶體結(jié)構(gòu)所含原子數(shù)保持穩(wěn)定,且均為面心立方FCC結(jié)構(gòu),這與彈性階段對(duì)應(yīng)。隨著應(yīng)變的增加,面心立方FCC結(jié)構(gòu)原子占比降低,與此同時(shí),體心立方BCC與六方密排HCP結(jié)構(gòu)原子占比增多,此時(shí)對(duì)應(yīng)應(yīng)力-應(yīng)變曲線的塑性激活區(qū)。整體上,300、600和900K的溫度下應(yīng)變分別達(dá)到17%、13%和8%時(shí),體系內(nèi)部FCC結(jié)構(gòu)原子占比開(kāi)始降低,300K下這種變化是突然發(fā)生的,但溫度越高,變化發(fā)生的越平緩。此外,無(wú)論此時(shí)體系溫度高低,FCC結(jié)構(gòu)原子占比最多,BCC與HCP結(jié)構(gòu)原子占比較少。當(dāng)應(yīng)變繼續(xù)增加,進(jìn)入應(yīng)力釋放階段后,在此階段3種晶體結(jié)構(gòu)的占比隨著應(yīng)變?cè)黾佣呌诜€(wěn)定。由此可見(jiàn),原子級(jí)微觀尺度下原子排布的變化直接影響著材料的應(yīng)力-應(yīng)變關(guān)系,這是因?yàn)镕CC結(jié)構(gòu)原子占比減小會(huì)導(dǎo)致體系內(nèi)部出現(xiàn)HCP與BCC結(jié)構(gòu),因此,引起位錯(cuò)、層錯(cuò)、滑移等結(jié)構(gòu)出現(xiàn)。此外,溫度越高,原子運(yùn)動(dòng)更活躍,從而降低了原子間結(jié)合力,更容易誘發(fā)體系內(nèi)部原子排序紊亂,更早地誘發(fā)不同類型位錯(cuò)的形核,最終體現(xiàn)在彈性模量與應(yīng)力-應(yīng)變曲線形貌的差別上。經(jīng)過(guò)以上分析可知,FCC結(jié)構(gòu)原子的演化會(huì)誘發(fā)晶體學(xué)缺陷,因此,在分析材料單軸拉伸形變機(jī)制時(shí)應(yīng)將完美的FCC結(jié)構(gòu)原子去除。借助位錯(cuò)提取算法(DislocationExtractionAlgorithm,DXA)對(duì)體系內(nèi)的位錯(cuò)類型及分布進(jìn)行分析,將分析結(jié)果與去除FCC結(jié)構(gòu)原子的體系相結(jié)合,以分析GH4169鎳基高溫合金的形變機(jī)制。圖4為3種溫度下不同應(yīng)變時(shí)的原子排列結(jié)構(gòu)及位錯(cuò)結(jié)構(gòu)特征,其中,片層狀原子為HCP結(jié)構(gòu),零星分布狀的單個(gè)原子為BCC結(jié)構(gòu),彌散團(tuán)簇狀與無(wú)序狀原子為無(wú)序結(jié)構(gòu)。同樣,以深淺不一的實(shí)線表征不同類型的位錯(cuò)。

從圖4中可以看出,位錯(cuò)的形核與運(yùn)動(dòng)使得體系內(nèi)部原子結(jié)構(gòu)重排,引發(fā)明顯的HCP結(jié)構(gòu)層錯(cuò)。層錯(cuò)與層錯(cuò)之間往往以一系列無(wú)序排列的原子為界。對(duì)于具有FCC結(jié)構(gòu)的GH4169鎳基高溫合金而言,內(nèi)部存在的堆垛層錯(cuò)可以等同于HCP結(jié)構(gòu),宏觀下結(jié)構(gòu)的演變表現(xiàn)為塑性形變。隨著應(yīng)變的增加,層錯(cuò)由塑性階段時(shí)體系兩端的多形核逐步向體系中間運(yùn)動(dòng),這證明此時(shí)會(huì)發(fā)生頸縮現(xiàn)象。位錯(cuò)大多出現(xiàn)于層錯(cuò)周圍,這是因?yàn)樵谕饬Φ淖饔孟?體系內(nèi)部異常排列的原子極易誘發(fā)位錯(cuò)形核,從而降低材料的力學(xué)性能。隨著應(yīng)變?cè)黾?位錯(cuò)的運(yùn)動(dòng)引導(dǎo)層錯(cuò)與層錯(cuò)之間的相互融合趨于穩(wěn)定,形成沿某個(gè)45°方向貫穿整個(gè)體系的層錯(cuò),即形成滑移。此外,位錯(cuò)運(yùn)動(dòng)會(huì)使異常排序的原子逐步演變成FCC結(jié)構(gòu),并且吸引異常排序的原子團(tuán)簇聚集于融合后的層錯(cuò)周圍,宏觀表現(xiàn)為塑性形變。需要注意的是,在形變過(guò)程中體系內(nèi)會(huì)出現(xiàn)由無(wú)序原子包裹的空位缺陷,這些空位可以被位錯(cuò)吸收,從而牽引位錯(cuò)與層錯(cuò)運(yùn)動(dòng),這與體系內(nèi)部不同結(jié)構(gòu)原子占比的變化相一致。另一方面,高溫下原子的劇烈運(yùn)動(dòng)會(huì)導(dǎo)致異常排序的原子增多,為位錯(cuò)形核提供了有利條件的同時(shí)增加了體系內(nèi)部空位的數(shù)量。這是因?yàn)閷?duì)于晶體材料而言,空位的形成會(huì)受到溫度的影響,溫度越高,空位形成的概率越大,在此情況下,位錯(cuò)及層錯(cuò)更容易發(fā)生運(yùn)動(dòng),與之對(duì)應(yīng)的是材料力學(xué)性能的下降。

2.3　形變過(guò)程中位錯(cuò)演化

圖5僅體現(xiàn)了體系內(nèi)部位錯(cuò)的類型及特征,以清楚地分析形變過(guò)程中位錯(cuò)的特征及演化。圖5a、圖5d與圖5g分別為300、600與920K溫度下原子結(jié)構(gòu)體系進(jìn)入塑性階段時(shí)的位錯(cuò)形貌、類型及分布。從圖5中可以看出,材料進(jìn)入塑性階段時(shí),位錯(cuò)主要以1/6<112>Shockley不全位錯(cuò)為主,與此同時(shí)存在1/2<110>Perfect全位錯(cuò)、1/6<110>Stair-rod壓桿位錯(cuò)、1/3<111>Frank分位錯(cuò)、1/3<100>Hirth分位錯(cuò)及其他位錯(cuò),不同類型的位錯(cuò)具有不同的柏氏矢量,并且1/3<111>Frank分位錯(cuò)及1/3<100>Hirth分位錯(cuò)的含量較小。從圖5a、圖5d與圖5g可以看出,材料剛進(jìn)入塑性階段時(shí)內(nèi)部位錯(cuò)長(zhǎng)度小、數(shù)量多,并且呈現(xiàn)點(diǎn)發(fā)射特征,這是因?yàn)?/6<112>Shockley不全位錯(cuò)是從空位表面發(fā)射,并且隨著應(yīng)變的增加,位錯(cuò)相互結(jié)合從而形成位錯(cuò)環(huán),此時(shí)部分1/6<112>Shockley不全位錯(cuò)在滑移面上以銳角相交時(shí)會(huì)形成1/6<110>Stair-rod壓桿位錯(cuò),而以鈍角相交時(shí)則會(huì)形成1/3<100>Hirth分位錯(cuò)。

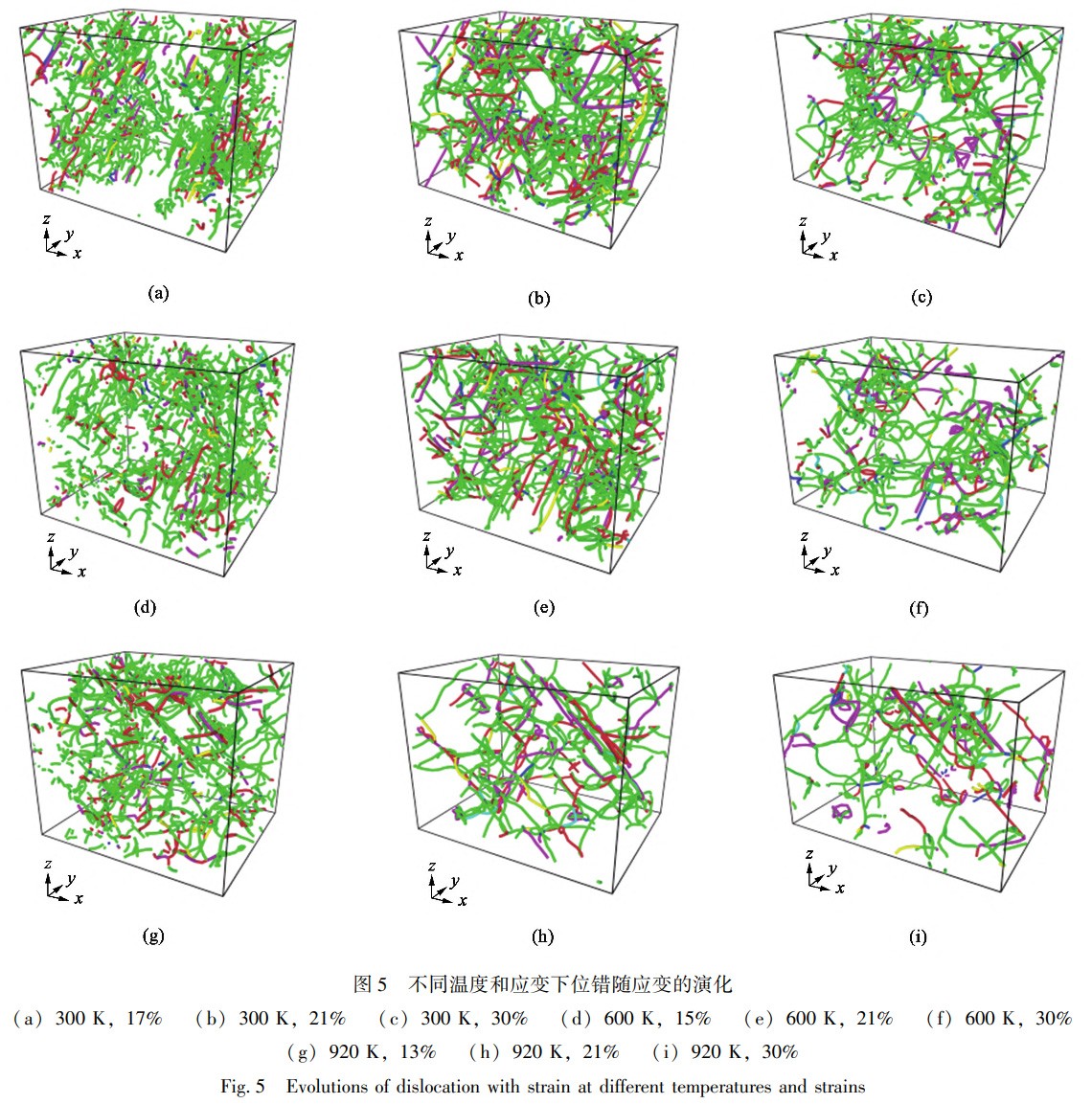
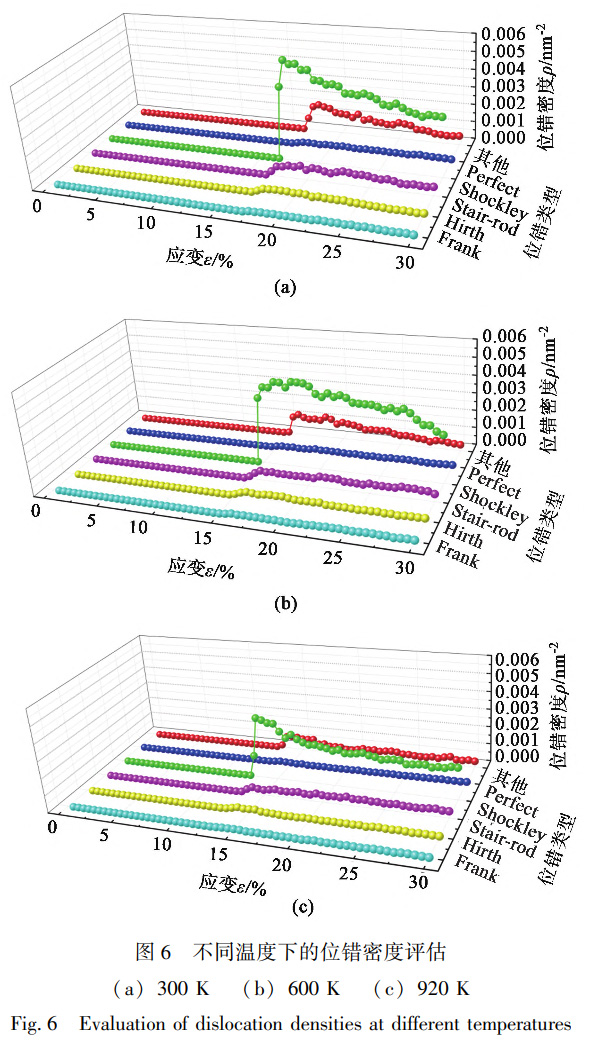
Shockley不全位錯(cuò)通常以刃形位錯(cuò)形式出現(xiàn),也可以是螺位錯(cuò)或混合型位錯(cuò),在外力作用下可以在{111}滑移面上運(yùn)動(dòng),從而牽引層錯(cuò)區(qū)擴(kuò)大或縮小,當(dāng)兩個(gè)層錯(cuò)區(qū)之間夾帶了一個(gè)定位錯(cuò)時(shí),會(huì)形成一個(gè)Stair-rod壓桿位錯(cuò),如圖5b、圖5e與圖5h所示。此外,還可以觀察到3種溫度下均會(huì)形成由多個(gè)Stair-rod壓桿位錯(cuò)包圍形成的位錯(cuò)環(huán),結(jié)合圖4可知,所圍區(qū)域?yàn)閷渝e(cuò)區(qū)域。由于Stair-rod壓桿位錯(cuò)屬于不可動(dòng)位錯(cuò),因此,一定程度上可以在塑性變形階段使材料發(fā)生硬化。應(yīng)變逐漸增大的同時(shí)位錯(cuò)也在不斷演化,在此過(guò)程中新的Stair-rod壓桿位錯(cuò)會(huì)形成,并且部分Stair-rod壓桿位錯(cuò)會(huì)發(fā)生解體與擴(kuò)散,演化為兩個(gè)可以進(jìn)行塑性形變的跟蹤位錯(cuò),即Shockley不全位錯(cuò),如圖5c、圖5f與圖5i所示。在整個(gè)拉伸形變過(guò)程中,體系內(nèi)部發(fā)生位錯(cuò)形核的同時(shí)也會(huì)出現(xiàn)空位,空位會(huì)引導(dǎo)位錯(cuò)運(yùn)動(dòng),位錯(cuò)運(yùn)動(dòng)又會(huì)形成新的空位,如此反復(fù),材料內(nèi)部的層錯(cuò)發(fā)生移動(dòng)和擴(kuò)展,最終導(dǎo)致滑移。對(duì)比不同溫度下的位錯(cuò)演化過(guò)程可知,溫度越高,位錯(cuò)形核位置越均勻,這是因?yàn)楦邷丨h(huán)境下體系內(nèi)部異常排布的原子的數(shù)量多,增大了位錯(cuò)形核的概率。此外,溫度越高,位錯(cuò)排布方向的一致性更高,且位錯(cuò)長(zhǎng)度更長(zhǎng),這是位錯(cuò)之間更加頻繁的相互作用導(dǎo)致的。對(duì)不同溫度和應(yīng)變時(shí)的位錯(cuò)密度進(jìn)行評(píng)估,結(jié)果如圖6所示。位錯(cuò)密度[12]計(jì)算公式如下:

式中:ρ為位錯(cuò)密度;ldis為體系中位錯(cuò)總長(zhǎng)度;V為原子結(jié)構(gòu)體積。從圖6可以看出,3種溫度下的總位錯(cuò)密度與應(yīng)力-應(yīng)變曲線具有一致的變化規(guī)律。彈性范圍內(nèi),隨著應(yīng)變的增加,體系內(nèi)部各類位錯(cuò)的數(shù)量均為0,當(dāng)材料進(jìn)入塑性階段時(shí),Shockley不全位錯(cuò)急劇增加,300、600與920K條件下Shockley不全位錯(cuò)密度的峰值分別為0.0057、0.0048與0.0033nm-2,位錯(cuò)密度的急劇升高證明了材料內(nèi)部出現(xiàn)了大量層錯(cuò)。隨后進(jìn)入應(yīng)力釋放階段,在此過(guò)程中Shockley位錯(cuò)密度持續(xù)降低,而其他類型的位錯(cuò)密度則有所升高,這是因?yàn)樾巫冞^(guò)程中Shockley位錯(cuò)之間不同的相互作用形式使其演化為其他類型位錯(cuò)。此時(shí)Stair-rod壓桿位錯(cuò)密度在相對(duì)穩(wěn)定的范圍內(nèi)波動(dòng),分別為0.0006、0.0005與0.0004nm-2,Stair-rod壓桿位錯(cuò)密度的相對(duì)穩(wěn)定證明了材料具有一定的抗變形能力。而造成這種波動(dòng)的原因是結(jié)構(gòu)為了可以在外力的作用下持續(xù)發(fā)生變形,迫使Stair-rod壓桿位錯(cuò)分解,與此同時(shí)又有新的Stair-rod壓桿位錯(cuò)形成。總體而言,相對(duì)較高的位錯(cuò)密度水平表明,形變過(guò)程中材料內(nèi)部位錯(cuò)反應(yīng)頻繁,并且滑移也較為活躍,尤其是在高溫環(huán)境下,位錯(cuò)的相互反應(yīng)更容易發(fā)生。

3、結(jié)論

(1)室溫(300K)、高溫(600和920K)的環(huán)境下,GH4169鎳基高溫合金的微觀彈性模量分別為125.9、125.3和119.1GPa,且彈性變形范圍內(nèi)的應(yīng)力-應(yīng)變曲線形貌差別不大,證明了GH4169鎳基高溫合金具有良好的高溫(920K)抗性。

(2)300、600和900K的溫度下應(yīng)變分別達(dá)到17%、13%及8%時(shí)體系內(nèi)部FCC結(jié)構(gòu)原子占比開(kāi)始降低,溫度越高,FCC結(jié)構(gòu)數(shù)量降低至最小值時(shí)的速率越低。依據(jù)體系內(nèi)部原子結(jié)構(gòu)的演化可將整體形變過(guò)程分為彈性區(qū)、塑性激活區(qū)及應(yīng)力釋放區(qū)。

(3)進(jìn)入塑性激活區(qū)后,大量Shockley不全位錯(cuò)形成,并且在隨后的形變過(guò)程中,Shockley不全位錯(cuò)密度逐漸降低,演化為其他類型位錯(cuò)。進(jìn)入應(yīng)力釋放區(qū)后,各類位錯(cuò)密度保持恒定,滑移的增多及運(yùn)動(dòng)使材料出現(xiàn)了頸縮現(xiàn)象。

參考文獻(xiàn):

[1]Plimpton S. Fast parallel algorithms for short-range molecular dynamics [J]. Journal of Computational Physics, 1995, 117: 1-19.

[2]Thompson A P, Aktulga H M, Berger R, et al. LAMMP—A flexiblesimulation tool for particle-based materials modeling at the atomic, meso, and continuum scales [ J ]. Computer Physics Communications, 2022, 271: 10817.

[3]Chen B, Wu W P, Chen M X, et al. Molecular dynamics study of fatigue mechanical properties and microstructural evolution of Nibasedsingle crystal superalloys under cyclic loading [J]. ComputationalMaterials Science, 2020, 185: 109954. [4] 　 Li N L, Wu W P, Nie K. Molecular dynamics study on the evolutionof interfacial dislocation network and mechanical properties of Ni-based single crystal superalloys [J]. Physics Letters A, 2018, 382: 1361-1367.

[5]Li X T, Peng S Y, Zhang X, et al. Microscopic and macroscopic analyses of the interaction mechanism between defect growth and dislocationemission in single-crystal aluminum [J]. Fatigue & Fractureof Engineering Materials & Structures, 2021, 44: 3008-3022.

[6]祝占偉. 鎳基合金中五重孿晶形成及變形機(jī)理的分子動(dòng)力學(xué)研究 [D]. 大連: 大連理工大學(xué), 2018. Zhun Z W. Study on the Formation and Deformation Mechanisms of Fivefold Twins in Nickel Base Alloy [D]. Dalian: Dalian Universityof Technology, 2018.

[7]Frakas D, Caro A. Model interatomic potentials for Fe-Ni-Cr-CoAlhigh-entropy alloys [J]. Journal of Materials Research, 2020, 35: 3031-3040.

[8]Nandy J, Yedla N, Gupta P, et al. Sintering of AlSi10Mg particlesin direct metal laser sintering process: A molecular dynamics simulation study [ J]. Materials Chemistry and Physics, 2019, 236: 121803.

[9]Wang J Q, Shin S, Hu A M, et al. Diffusion kinetics of transient liquid phase bonding of Ni-based superalloy with Ni nanoparticles: A molecular dynamics perspective [ J]. Computational Materials Science, 2018, 152: 228-235.

[10]Wu W P, Yao Z Z. Molecular dynamics simulation of stress distributionand microstructure evolution ahead of a growing crack in singlecrystal nickel [J]. Theoretical and Applied Fracture Mechanics,2012, 62: 67-75.

[11]楊攀峰. Ni-Co 合金拉伸力學(xué)性能和變形機(jī)制的模擬研究[D]. 蘭州: 蘭州理工大學(xué), 2020.

Yang P F. The Simulation Research of Tensile Mechanical Propertiesand Deformation Mechanism of Ni-Co Alloys [D]. Lanzhou: Lanzhou University of Technology, 2020.

[12] Li L, Shen L M, Proust G. Fatigue crack initiation life prediction for aluminium alloy 7075 using crystal plasticity finite element simulations [J]. Mechanics of Materials, 2015, 81: 84-93.

相關(guān)鏈接